Derrick Lee's Blog

在现代金融活动中，借贷是一种最常见的方式。借贷经过各种包装和杠杆，就形成了各式各样的金融产品。本文以P2P系统中的等额本息借贷关系为例，讨论如何保证金额在不同流程中计算的准确性。

一般来说，投资人的回款计划，以及借款人的还款计划会在项目成立（也就是满标），放款完成之后生成。在后续的所有流程中，均不会更改已生成的金额数据，比如在还款成功之后，只会变更计划的状态为已还清。对于本文中可能会出现的名词，现如下定义：

投资人：出钱的人。当借贷关系成立时，为资金流出方，当借贷关系结束时，为资金流入方。

借款人：借钱的人。当借贷关系成立时，为资金流入方，当借贷关系结束时，为资金流出方。

标的：将借款人的需求包装而成的金融产品。

投资：投资成功后，投资人账户金额会被冻结。

放款：当标的成立之后，托管机构将钱从投资人账户转到借款人账户。

还款：借款人将本息通过托管机构还给投资人。

资金端：拥有投资人资源，提供资金来源。

资产端：拥有借款人资源，提供借款需求。

c compile

图片来源

等额本息算法定义

重要说明：等额本息的重点在于每月偿还本息一致，或者还款总额一致。不同机构给出的计划的利息、本金、剩余本金明细可能不完全一致，比如新浪理财计算器，与招商银行贷款计算器在金额10000元，利率10%，期限12个月的情况下就不完全一致，如下图所示：

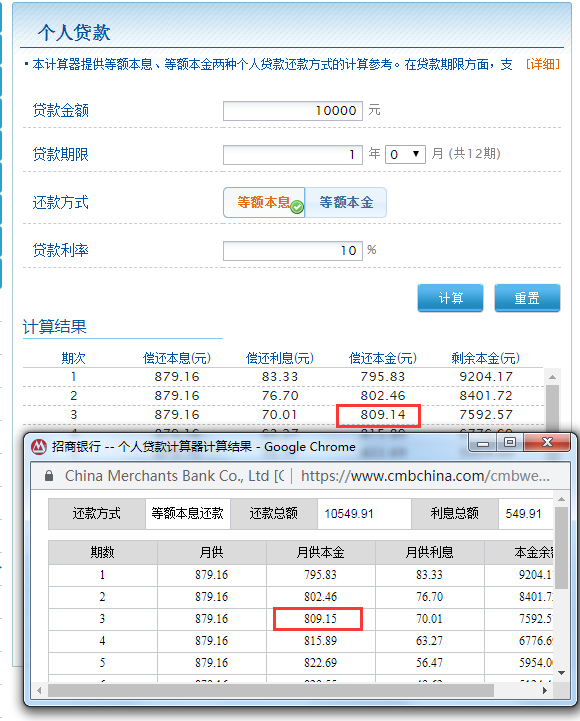
c compile

本文所采用的算法伪代码描述如下：

定义剩余本金p = 借款金额

计算出每月应还本息总额n

对每一期做如下计算：

{

非最后一期，计算出每月应还利息为m，应还本金为n - m

最后一期，当期应还本金为剩余本金p，应还利息为n - p

p = p - 当期应还本金

第i期剩余本金 = p

}

完整Java代码如下所示：

/**
 * 等额本息，计算每月应收或者应还总额
 *
 * @param amount 金额基数
 * @param rate 利率
 * @param period 总月数
 */
public static BigDecimal calculateMonthTotal(BigDecimal amount, BigDecimal rate, int period) {
    //月利率
    double monthRate = rate.doubleValue() / 100 / 12;
    //每月回款总额，等于本金 + 利息
    return amount.multiply(new BigDecimal(monthRate * Math.pow(1 + monthRate, period)))
            .divide(new BigDecimal(Math.pow(1 + monthRate, period) - 1), 2, BigDecimal.ROUND_HALF_UP);
}

public static List<Plan> calculateInvestPlan(BigDecimal investAmount, BigDecimal rate, int period) {
    //月利率
    double monthRate = rate.doubleValue() / 100 / 12;
    //每月回款总额，等于本金 + 利息
    BigDecimal monthIncome = calculateMonthTotal(investAmount, rate, period);
    BigDecimal monthInterest;
    BigDecimal remainPrincipal = investAmount;
    List<Plan> investIncomeList = new ArrayList<>(period);
    for (int i = 1; i <= period; i++) {
        BigDecimal multiply = investAmount.multiply(new BigDecimal(monthRate));
        BigDecimal sub = new BigDecimal(Math.pow(1 + monthRate, period)).subtract(new BigDecimal(Math.pow(1 + monthRate, i - 1)));
        //每月利息
        monthInterest = multiply.multiply(sub).divide(new BigDecimal(Math.pow(1 + monthRate, period) - 1), 2, BigDecimal.ROUND_HALF_UP);
        Plan investIncome = new Plan();
        investIncome.setTotal(monthIncome);
        investIncome.setPeriod(i);
        if (i < period) {
            //不是最后一期
            investIncome.setPrincipal(monthIncome.subtract(monthInterest));
            investIncome.setInterest(monthInterest);
        } else {
            //最后一期做差值
            investIncome.setPrincipal(remainPrincipal);
            investIncome.setInterest(monthIncome.subtract(investIncome.getPrincipal()));
        }
        remainPrincipal = remainPrincipal.subtract(investIncome.getPrincipal());
        investIncome.setOutstanding(remainPrincipal);
        investIncomeList.add(investIncome);
    }
    return investIncomeList;
}

public static class Plan {
    //当前期数
    private int period;
    //当期本金
    private BigDecimal principal;
    //当期利息
    private BigDecimal interest;
    //剩余本金
    private BigDecimal outstanding;
    //应还总额
    private BigDecimal total;

    //gets and sets
}

代码清单1

无中介费的情况

在明确了使用的算法之后，首先考虑无中介费用的情况，也就是sum(投资人收益) = 借款人成本。先计算出每个投资人的回款计划，比如：

//投资人1回款计划
List<Plan> investIncomeList = calculateInvestPlan(new BigDecimal("10000"), new BigDecimal("10"), 12);
//投资人2回款计划
List<Plan> investIncomeList2 = calculateInvestPlan(new BigDecimal("23000"), new BigDecimal("10"), 12);

借款人的还款计划不需要计算，只需累加投资人的数据即可。算法伪代码描述如下：

定义剩余本金p = 借款金额

对借款人每一期数据做如下计算：

{

第i期应还本金 = sum(所有投资人第i期应收本金)，第i期应还利息 = sum(所有投资人第i期应收利息)

p = p - 当期应还本金

第i期剩余本金 = p

}

完整代码如下所示：

/**
 * 计算借款人还款计划
 *
 * @param amount 借款金额
 * @param period 总期数
 * @return
 */
public static List<Plan> calculateRepayPlan(BigDecimal amount, int period) {
    //借款人还款计划
    BigDecimal remainPrincipal = amount;
    List<Plan> repayPlanList = new ArrayList<>(period);
    for (int index = 0; index < period; index++) {
        Plan totalSum = calculateSumInvestPlan(index + 1);
        Plan repayPlan = new Plan();
        repayPlan.setInterest(totalSum.getInterest());
        repayPlan.setPrincipal(totalSum.getPrincipal());
        remainPrincipal = remainPrincipal.subtract(repayPlan.getPrincipal());
        repayPlan.setOutstanding(remainPrincipal);
        repayPlanList.add(repayPlan);
    }
    return repayPlanList;
}

代码清单2

有中介费的情况

当然在实际情况中，服务费是普遍存在的，这也是网贷中介收入的来源之一（监管规定总费率不能超过36%），而此时标准的等额本息公式已经不再适用了。在标准公式中，只存在本金和利息的计算，为了让借款人和投资人的计划表的每月总额符合等额本息，需要取巧。假设有服务费A为2%，服务费B为3%，且要和基础利率10%一起做等额本息计算，算法伪代码如下所示：

定义剩余本金p = 借款金额

计算出借款人每月应还总额n

对借款人每一期数据做如下计算：

{

第i期应还本金pi = sum(所有投资人第i期应收本金)，第i期应还利息ii = sum(所有投资人第i期应收利息)

第i期总服务费k = n - pi - ii

//服务费K如何分配，可以自行定义，可以按照比例均摊，比如：

第i期服务费A = 向下取整(k * 2 / 3)，第i期服务费B = k - 第i期服务费A

p = p - 当期应还本金

第i期剩余本金 = p

}

采用向下取整是为了防止费用总类很多时，只入不舍，造成最后一期费用为负数。完整代码如下所示：

/**
 * 计算借款人还款计划，有服务费
 *
 * @param amount 借款金额
 * @param period 总期数
 * @return
 */
public static List<Plan> calculateRepayPlanWithFee(BigDecimal amount, BigDecimal rate, int period, BigDecimal feeA, BigDecimal feeB) {
    //借款人还款计划
    BigDecimal remainPrincipal = amount;
    List<Plan> repayPlanList = new ArrayList<>(period);
    BigDecimal monthRepay = calculateMonthTotal(amount, rate, period);
    BigDecimal totalServiceFeeRate = feeA.add(feeB);
    for (int index = 0; index < period; index++) {
        Plan totalSum = calculateSumInvestPlan(index + 1);
        Plan repayPlan = new Plan();
        repayPlan.setInterest(totalSum.getInterest());
        repayPlan.setPrincipal(totalSum.getPrincipal());
        remainPrincipal = remainPrincipal.subtract(repayPlan.getPrincipal());
        repayPlan.setOutstanding(remainPrincipal);
        BigDecimal totalServiceFee = monthRepay.subtract(totalSum.getTotal()).setScale(2, BigDecimal.ROUND_DOWN);
        //存在手续费，各手续费按利率的比例分配
        BigDecimal manageFeeA = feeA.divide(totalServiceFeeRate, 2, BigDecimal.ROUND_HALF_UP).multiply(totalServiceFee).setScale(2, BigDecimal.ROUND_DOWN);
        repayPlan.setManagerFeeA(manageFeeA);
        totalServiceFee = totalServiceFee.subtract(manageFeeA);
        repayPlan.setManagerFeeB(totalServiceFee);
        repayPlanList.add(repayPlan);
    }
    return repayPlanList;
}

代码清单3

存在问题

由于借款人的还款计划由投资人的回款计划汇总而来，与标准公式计算出来的还款计划可能存在明细上的差别。依然使用本文的例子，考虑如下情况：

投资人1投资了10000元，回款计划表如下所示：

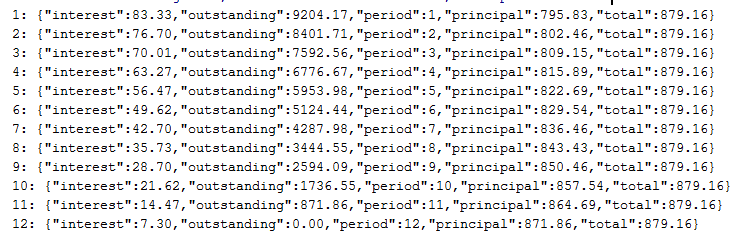
c compile

表1 投资人1回款计划

投资人2投资了23000元，回款计划表如下所示：

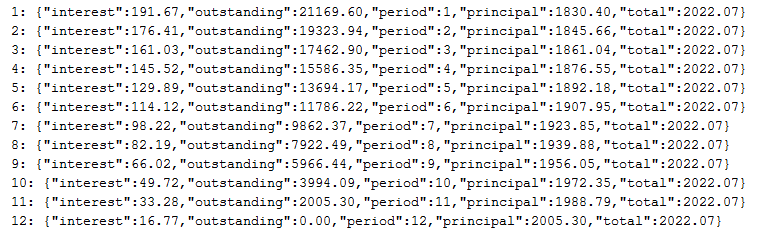
c compile

表2 投资人2回款计划

借款人投资了33000元，还款计划表如下所示：

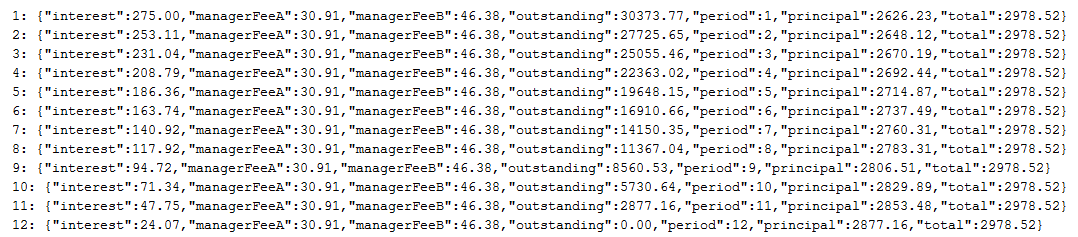
c compile

表3 用15%生成的还款计划

在表3中，每月应还总额是标准值，但是利息和本金却是非标准的，原因是在生成每个投资人的每期数据时，都会进行四舍五入。当我们用10%的利率做33000元12期等额本息时，每一期只会做一次四舍五入。多次舍入和一次舍入，是造成差异的根本原因。

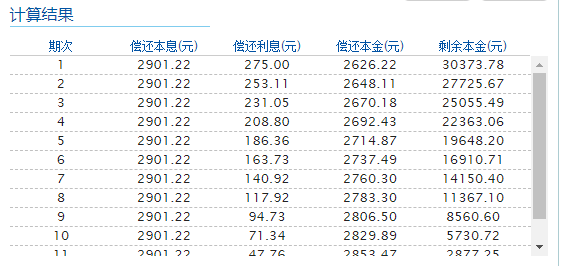
c compile

表4 用10%生成的还款计划

在表3和表4中，每一期的本金或者利息都有些许不一致。但笔者认为这种差异不算问题，原因如下：

等额本息应优先关注总额而非明细，除非明细相差特别大。
如果以借款人优先的角度，先计算借款人还款计划，可以解决还款计划非标的问题。但在生成投资人回款计划时，势必也会出现某个回款计划非标的情况，这是不可调和的。

总结

1. 本文从投资人优先的角度，先计算投资人的计划数据，再由此生成借款人的计划数据。由一份数据源，再生产后续所需的数据源，从而保证了金额的准确性。在计算借款人计划时，不能再运用等额本息公式进行计算，否则会因为精度问题导致每期还款总额与出借人应收总额不一致。如果资产端从借款人角度分析还款计划，会发现有细微查别，但笔者认为这不是错误。

2. 如果需要把某一个数total摊为n期，建议在1～n-1期都用向下取整（只舍不入），并在第n期的值设为total - sum(1~n-1)，这样可以保证1～n期的总和准确，并且第n期不会成为负数。

3. 由于除了本金和利息之外的费用都不属于标准等额本息公式的范畴，如何分配这些费用依各方自身需求而定，本文采用的是按比例均摊。

4. 本文同时涉及资金端和资产端，在实际系统中两边资金流的出入必须对应，并且金额准确。在本文中，借款人第i期的还款总额 = sum(所有投资人第i期)。

附件

本博文所展示的源代码由此获得。

参考链接

[1] 等额本息[EB/OL].https://baike.baidu.com/item/%E7%AD%89%E9%A2%9D%E6%9C%AC%E6%81%AF，2019-07-30.
[2] 理财计算器[EB/OL].http://finance.sina.com.cn/calc/money_loan.html，2019-07-30.
[3] 个人贷款计算器[EB/OL].https://www.cmbchina.com/CmbWebPubInfo/Cal_Loan_Per.aspx?chnl=dkjsq，2019-07-30.

Stay foolish, Stay ugly

Recent Posts

Links

一种精确的理财金额算法的设计与实现（以等额本息为例）

等额本息算法定义

无中介费的情况

有中介费的情况

存在问题

总结

附件

参考链接